 2011-2012
2011-2012
A man wants to build a rectangular enclosure for his herd. He only has $900 to spend on the fence and wants the largest size for his money. He plans to build the pen along the river on his property, so he does not have to put a fence on that side. The side of the fence parallel to the fence will cost $5 per foot to build, whereas the sides perpendicular to the river will cost $3 per foot. What dimensions should he choose?
Solution:
Start by drawing a picture of the situation.
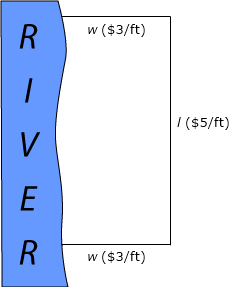
According to the problem, the farmer is attempting to maximize the size of the rectangular plot. Therefore, the primary equation will be area: A = l ∙ w. However, to take the derivative (maximizing the function), you need to eliminate a variable, either l or w; for that, you’ll need a secondary equation.
You know he wants to spend $900. Furthermore, each foot of the 2 fences he’ll use for the width of the yard will cost $3. Each foot of the fence parallel to the river will cost $5.
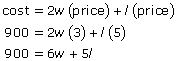
Solve the cost equation for one of its variables; I’ll solve for l.
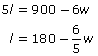
Now plug this in for l in the primary area equation.
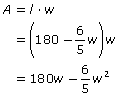
Now that you’ve got one variable, maximize by finding the derivative and setting it equal to 0.
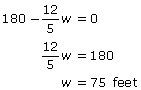
To find the corresponding length of the optimized field, plug 75 in for w into the modified secondary equation.
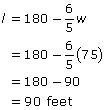
So the optimized field has a fence parallel to the river measuring 90 feet and two other fences connecting it to the river that measure 75 feet each.
The video may take a few seconds to load.Having trouble Viewing Video content? Some browsers do not support this version – Try a different browser.






